![\includegraphics[%
scale=0.6]{/home/lalo/DOC/WWW/tudomanyfilozofia/Eloadas/michelson.eps}](img2.gif)
Tegyük fel, hogy az ábrán látható berendezés az éterhez (Éter= egy
olyan feltételezett közeg, amelyben az elektromágneses hullámok terjednek,
![]() sebességgel, és amelyhez rögzített vonatkoztatási
rendszerben Maxwell igaznak tételezte a Maxwell-egyenleteket.) képest
sebességgel, és amelyhez rögzített vonatkoztatási
rendszerben Maxwell igaznak tételezte a Maxwell-egyenleteket.) képest
![]() sebességgel halad a - a Földdel együtt. A forrásból kilépő fénysugarat
egy féligáteresztő tükörrel két részre bontjuk. A két kart oda és
vissza befutva a sugarak találkoznak, és a két futási idő különbségétől,
sebességgel halad a - a Földdel együtt. A forrásból kilépő fénysugarat
egy féligáteresztő tükörrel két részre bontjuk. A két kart oda és
vissza befutva a sugarak találkoznak, és a két futási idő különbségétől,
A MM kísérlet null eredménye következtében előállt krízis megoldódásával kapcsolatban a következő, széles körben elterjedt álláspontokat különböztetjük meg:
Mi történik egy ponttöltéssel, ha mozgásba hozzuk? Erre a Maxwell-egyenletek pontos választ adnak:
![\includegraphics[%
scale=0.6]{/home/lalo/DOC/WWW/tudomanyfilozofia/Eloadas/erovonalak.eps}](img9.gif)
Ebből az effektusból levezethető, hogy
![\includegraphics[%
width=6cm,
height=7cm]{/home/lalo/DOC/WWW/tudomanyfilozofia/Eloadas/michelson.eps}](img12.gif)
Így ,,látná'' (hogy mit látna, az egy kicsit bonyolultabb
kérdés, de ilyen deformáltnak állapítaná meg) a MM berendezést egy
olyan megfigyelő, akihez képest ![]() sebességgel mozog (mondjuk, aki
áll az éterhez képest). Ez szemmel láthatóan megmagyarázza a null
eredményt. Más szóval, nincs semmi meglepő a MM kísérlet eredményében,
pontosan azt tapasztaljuk, amit tapasztalnunk kell a klasszikus fizikából
kiszámolva! Mi, a MM berendezéssel együtt mozgó megfigyelők nem tapasztaljuk
ezt a deformációt, mert a méterrúdjaink ugyanúgy deformáltak, a retinánk
ugyanúgy deformált, stb. (Deformáció alatt azt értjük, milyen ahhoz
képest, ha az éterben állna.)
sebességgel mozog (mondjuk, aki
áll az éterhez képest). Ez szemmel láthatóan megmagyarázza a null
eredményt. Más szóval, nincs semmi meglepő a MM kísérlet eredményében,
pontosan azt tapasztaljuk, amit tapasztalnunk kell a klasszikus fizikából
kiszámolva! Mi, a MM berendezéssel együtt mozgó megfigyelők nem tapasztaljuk
ezt a deformációt, mert a méterrúdjaink ugyanúgy deformáltak, a retinánk
ugyanúgy deformált, stb. (Deformáció alatt azt értjük, milyen ahhoz
képest, ha az éterben állna.)
Lorentz (Poincaré és Larmor. Hogy pontosan ki, mikor és mit, az részletesebb
történeti áttekintést igényelne. Mivel ez minket most nem érdekel,
az egyszerűség kedvéért mindent Lorentz-nek tulajdonítok.) azt is
észrevette, hogy az éterhez viszonyított mozgás hatása a fizikai rendszerek
viselkedésére egy sajátos törvényszerűséget mutat: nevezetesen a mozgó
fizikai rendszerre vonatkozó számolás eredménye érdekes alakot ölt,
ha az eredményt a következő új változókban fejezzük ki:
| (1) |
A mozgó fizikai rendszer viselkedését megkapjuk, ha az ugyanilyen álló rendszer viselkedésére vonatkozó feladatot oldjuk meg, és az eredményekben elvégezzük aFontos a későbbiek szempontjából az a könnyen belátható tény, hogy ezek az új változók nem mások, mint azok az ,,idő'' és ,,tér'' (Az idézőjel - legalábbis Lorentz számára - nagyon fontos!) koordináták, melyeket a mozgó objektumhoz rögzített vonatkoztatási rendszerbeli - vagyis mozgó, és így deformált - órákkal és méterrudakkal mérnénk. Így a Lorentz-elvet a következőképpen is kimondhatjuk:helyettesítést.
A fizika törvényei olyanok, hogy bármely fizikai rendszer az éterhez viszonyított mozgás hatására úgy deformálódik (értsd ez a mozgás úgy módosítja a rendszer viselkedésére vonatkozó, a fizika szokásos törvényeiből levezetett eredményeket), hogy ebből az eredményből nem állapítható meg egyetlen vonatkoztatási rendszernek sem az éterhez viszonyított sebessége.Tanulságos végiggondolnunk, hogy hogyan néz ki a világ, a Lorentz-elméletet alapul véve, egy, az éterhez képest mozgó megfigyelő számára.![[*]](file:/usr/local/share/lib/latex2html/icons/footnote.gif)
A mozgó megfigyelőre vonatkozó kérdés nem teljesen akadémikus. Nem rakétákban száguldó emberekre kell gondolni, hanem arra, hogy magát a Nap körül keringő Földet jó okunk van - legalábbis az év nagy részében - mozgó vonatkoztatási rendszernek tekintenünk. A lényeg, amit a Lorentz-invariancia alapján a mozgó megfigyelőről meg kell állapítanunk, hogy azok a vesszős változók, melyeket a fentiekben csupán matematikai segédletként vezettünk be, nem mások, mint amiket egy állandó sebességgel mozgó, ugyanakkor magát nyugvónak képzelő megfigyelő természetes módon a helyes változóknak gondol. Továbbá, a fizika törvényei ezekben a változókban kifejezve pontosan úgy festenek, mint ahogyan azt a mozgó megfigyelő, még amikor nyugalomban volt, az iskolában megtanulta (feltéve, hogy helyesen tanították meg neki). Egy ilyen megfigyelő, hívjuk őt mondjuk Alice-nek, természetes módon egy hozzá képest nyugvó pontot fog koordinátarendszere origójául választani. Ezzel pontosan rögzítettük atagot a
összefüggésben. Alice méterrúdjai pedig pontosan afaktornak megfelelő mértékű Fitzgerald-kontrakciót szenvedik el. De hogy lehet, hogy nem látja, hogy a méterrúdjai összehúzódnak amikor
irányba fekteti őket, és meghosszabbodnak, amint
irányba elforgatja? Ennek az a magyarázata, hogy Alice szemének retinája szintén kontrahálódik, és így ugyanazok a sejtek érzékelik a méterrúd képét, mintha a rúd is és a megfigyelő is nyugalomban lenne. Hasonlóképpen, Alice nem érzékeli, hogy órája lelassult, mert ezzel együtt lelassult saját gondolkodásának ritmusa is. Továbbá arról sem fog tudni - hiszen magát nyugalomban lévőnek képzeli -, hogy a tőle távolodó és feléje közelítő fényjelek különböző,
, relatív sebességgel haladnak. Ez aztán ahhoz vezet, hogy Alice helytelenül szinkronizálja az egymástól távoli órákat, és végül azt fogja hinni, hogy a
a valódi idő, már csak azért is mert ezzel a választással úgy tűnik számára, hogy a fény terjedési sebessége minden irányban.
Mindezek után Alice ellenőrizheti a fizika törvényeit, és örömmel tapasztalhatja, hogy azok pontosan olyanok, mint ahogyan emlékszik rájuk, s hogy az alkalmazott definíciók és eljárások jól működnek. Ha valami mégsem stimmel, akkor hamar rájön, hogy valamelyik berendezése meghibásodott (például megrongálódott a gyorsítás során), és megjavítja. Tekintsünk most egy álló megfigyelőt, Bobot. Mivel Alice magát nyugalomban lévőnek hiszi, úgy gondolja, hogy Bob az, aki mozog. És könnyen kifejezhetjük az Alice által használt változókat a Bob által használtakkal, és viszont, csakelőjelét kell megváltoztatni:
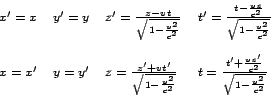
Alice azt állítja majd, hogy Bob méterrúdjai kontrahálódtak, órája lassabban jár, és hogy Bob helytelenül szinkronizálta az egymástól távoli órákat. Alice, megértően úgy gondolja majd, hogy Bob azért használ rossz változókat, mert műszerei Fitzgerald-Larmor-Lorentz-Poincaré-kontrakciót szenvedtek. Ahogyan Alice látja a világot, az logikailag teljesen konzisztens, és tökéletes összhangban van a megfigyelt tényekkel. Bobnak semmi esélye sincs, hogy meggyőzze tévedéséről.Bell elemzéséből kitűnik, hogy téves az a gyakori ellenvetés, hogy a Lorentz-elmélet nem képes számot adni egy álló rúdnak a mozgó megfigyelő rendszerében tapasztalt kontrakciójáról, hiszen - szól az ellenérv - az álló rúd kontrakcióját nem okozhatták a Lorentz által feltételezett, az éterhez viszonyított mozgásból származó fizikai deformációk. A fenti elemzés világosan megmutatta, hogy az álló rúdnak a mozgó megfigyelő által észlelt kontrakciója nagyon is jól értelmezhető, méghozzá éppen a mozgó megfigyelő mozgó méterrúdjaiban és mozgó óráiban bekövetkezett fizikai deformációk következményeként.
Mindezek tükrében, hogyan definiálná a klasszikus fizika embere a
tér- és időkoordinátákat egy a Párizsi Szabványügyi Hivatal vitrinjéhez
(ahol a méterrudat őrzik, és a játék kedvéért most tegyük fel, hogy
egy etalon órát is őriznek) képest ![]() sebességgel mozgó vonathoz
rögzített vonatkoztatási rendszerben?
sebességgel mozgó vonathoz
rögzített vonatkoztatási rendszerben?
![\includegraphics[%
scale=0.45]{/home/lalo/DOC/WWW/tudomanyfilozofia/Eloadas/kocsi_HU.eps}](img25.gif)
Analógia: Hogyan járnánk el, ha az etalon méterrúddal, amelynek a
hiteles hossza
![]() -os hőmérsékleten van
értve, olyan helyen kell mérnünk, ahol a hőmérséklet
-os hőmérsékleten van
értve, olyan helyen kell mérnünk, ahol a hőmérséklet
![]() ,
és tudjuk, hogy a hőtágulási törvényből kiszámolhatóan, ezen a hőmérsékleten
a hossza csak
,
és tudjuk, hogy a hőtágulási törvényből kiszámolhatóan, ezen a hőmérsékleten
a hossza csak
![]() ? Nyilván úgy, hogy ha valamire a
méterrúd hatszor fér rá, akkor azt mondjuk, hogy a hossza
? Nyilván úgy, hogy ha valamire a
méterrúd hatszor fér rá, akkor azt mondjuk, hogy a hossza
![]() .
.
Hasonlóan, a klasszikus fizika tér- és időszemlélete szerint
A távoli események egyidejűségének definíciójánál figyelembe vesszük,
hogy a kezdetben szinkronizált órák elmozdítása során elállítódnak
(ami ekvivalens annak figyelembevételével, hogy a fényjelek nem ugyanolyan
sebességgel haladnak egyik illetve a másik irányba, ha fényjelekkel
szinkronizálunk.). Az így definiált tér- és időkoordinátákkal tökéletesen
megvagyunk, minden leírható, és a világ ![]() térképe egy euklideszi
geometriával írható le. Az egyidejűség fogalma nem függ a vonatkoztatási
rendszertől, stb.
térképe egy euklideszi
geometriával írható le. Az egyidejűség fogalma nem függ a vonatkoztatási
rendszertől, stb.
A relativitáselmélet lényege, hogy ezen a ponton a következő javaslatot
teszi: Hagyjuk a csudába ezeket a korrekciókat, ne törődjünk azzal,
hogy a méterrudak deformálódtak, és az órák lelassultak, hanem definiáljuk
az etalonokhoz képest mozgó vonatkoztatási rendszerben a tér- és időkoordinátát
úgy, mintha semmi sem deformálódott volna:
Továbbá a távoli események egyidejűségének definíciójakor sem veszünk
tudomást arról, hogy az órák transzportja során azok elállítódnak
(másik módszer esetén, hogy a fényjelek oda és vissza más sebességgel
haladnak a vonathoz képest). Mármost világos, hogy ![]() és
és ![]() egymásból könnyen kifejezhetők, és a fizika törvényeit kedvünk szerint
egyaránt jól felírhatjuk
egymásból könnyen kifejezhetők, és a fizika törvényeit kedvünk szerint
egyaránt jól felírhatjuk ![]() és
és ![]() változókban is. A világ
változókban is. A világ
![]() -térképe egy Minkowski-geometria.
-térképe egy Minkowski-geometria.
Két elmélet azonos, ha mindenről ugyanazt mondja. A klasszikus fizika
az ![]() változók értékeiről, illetve ezek tetszőleges
változók értékeiről, illetve ezek tetszőleges ![]() függvényeiről (pl.
függvényeiről (pl.
![]() ) is, és az
) is, és az ![]() változók értékeiről, illetve ezek tetszőleges
változók értékeiről, illetve ezek tetszőleges ![]() függvényeiről
(pl.
függvényeiről
(pl.
![]() ) is ugyanazt állítja, mint
a relativitáselmélet. A két elmélet között kizárólag nyelvi
különbség van: a klasszikus fizika
) is ugyanazt állítja, mint
a relativitáselmélet. A két elmélet között kizárólag nyelvi
különbség van: a klasszikus fizika ![]() -et nevezi ,,tér''-koordinátának
és
-et nevezi ,,tér''-koordinátának
és ![]() -t ,,idő''-koordinátának, a relativitáselmélet pedig
-t ,,idő''-koordinátának, a relativitáselmélet pedig ![]() -t
és
-t
és ![]() -t.
-t.
Ami az inkommenzurábilitási tézis szempontjából fontos: az egyik elméletben empirikusan értelmezett fogalmak ugyanazok, mint a másikban (pontosabban mindkettőben minden értelmezhető, ha akarjuk, az összevetés céljából), és ezért tökéletesen összevethetők, vagyis létezik az a Kuhn és Feyerabend és mások által tagadott invariáns empirikus ,,nyelv'', amely lehetővé teszi az összevetésüket! (Ráadásul, mint látjuk, nemhogy összevethetők, hanem egyenesen azonosak!)
Példa: Számoljuk ki, mekkora úton lehetne egy elektront felgyorsítani a fénysebesség 90%-ra, ha a nem lenne igaz a tömegformula, azaz - mint korábban hittük - a tömeg nem függ a sebességtől.
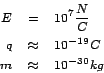
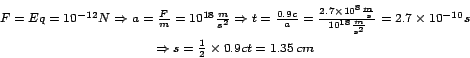
Ehhez képest a Stanfordi Lineáris Gyorsító ![]() hosszú, és
300 millió dollárba került! (Ez pontosan az a hosszúság, amit az
hosszú, és
300 millió dollárba került! (Ez pontosan az a hosszúság, amit az
![]() formulából számolunk.) Nehéz lenne azt mondani, hogy empirikus alapon
nem dönthető el, melyik elmélet a helyes, az
formulából számolunk.) Nehéz lenne azt mondani, hogy empirikus alapon
nem dönthető el, melyik elmélet a helyes, az
![]() ,
vagy az
,
vagy az
![]() !
!